27 An Introduction to Facility Location Problems
One job of budding Data Scientists is to help their organisations in making decisions when it comes to deciding about the locations for services.
Real life healthcare examples may include
- reviewing (and rationalising) existing service locations
- providing a comparison of the pros and cons of several proposed sites for a service
- suggesting optimal locations for new services to best tackle existing inequalities or areas of poor access
- suggesting which existing services can be closed down while having the least impact on access and equality
“In health care, the implications of poor location decisions extend well beyond cost and customer service considerations.
If too few facilities are utilized and/or if they are not located well, increases in morbidity (infections) can have a major impact on public health.
Thus, facility location modelling takes on an even greater importance when applied to the siting of health care facilities.”
27.1 An example: sexual health clinics in Hampshire
Meskarian R, Penn ML, Williams S, Monks T (2017) A facility location model for analysis of current and future demand for sexual health services. PLoS ONE 12(8): e0183942.
https://doi.org/10.1371/journal.pone.0183942
The project aimed to assist in planning the sexual health service provision in Hampshire.
They forecast future demand for different aspects of the service over the next 3–5 years, based on population age and gender projections published by the council.
They performed a facility location analysis based on the current and forecasted demand to identify an optimal number of clinics and their geographic location.
The project aimed to reduce the number of clinics while maintaining/improving service access

There were 278 ‘demand points’ where people could be coming from - these were all of the postcode sectors.
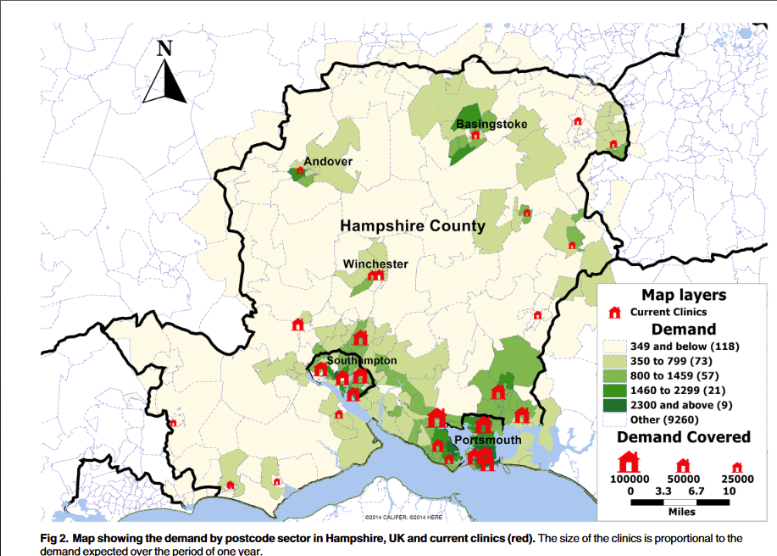
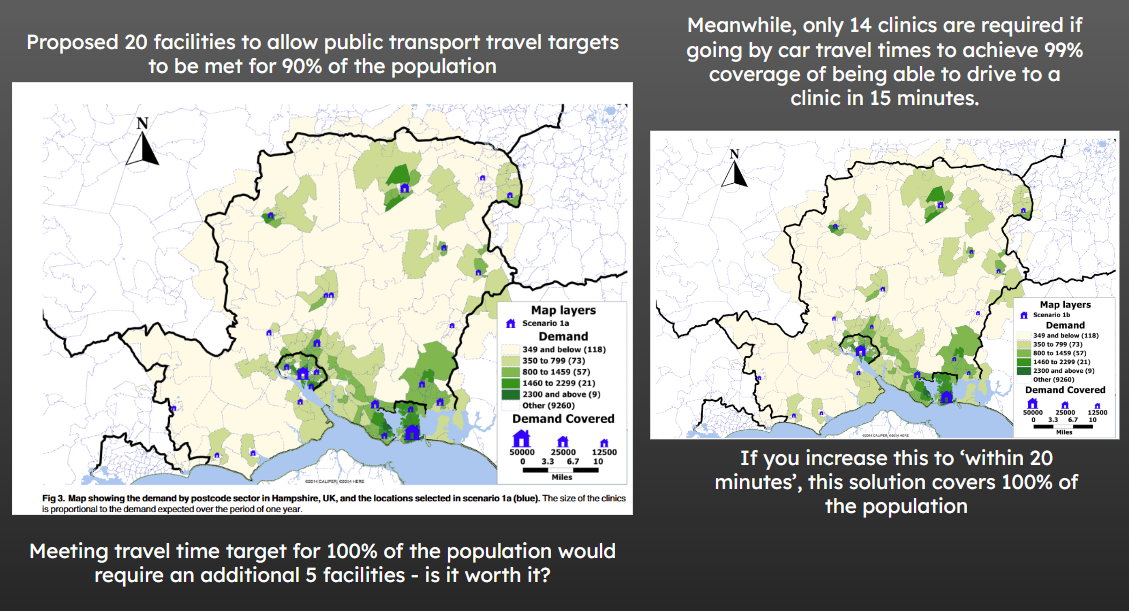
27.1.1 Findings
The clinic locations could be reduced from 28 to 20 and still keep 90% of all patient journeys by public transport (e.g. by bus or train) to a clinic within 30 minutes.
The number of clinics could be further reduced to 8 if the travel time is based on car travel times within 15 minutes.
27.1.2 Limitations
The public transport analysis assumed everyone would travel by public transport - but this is unrealistic (and census data showed over 85% of the population across the county having access to 1+ cars)
27.1.3 Diminishing returns
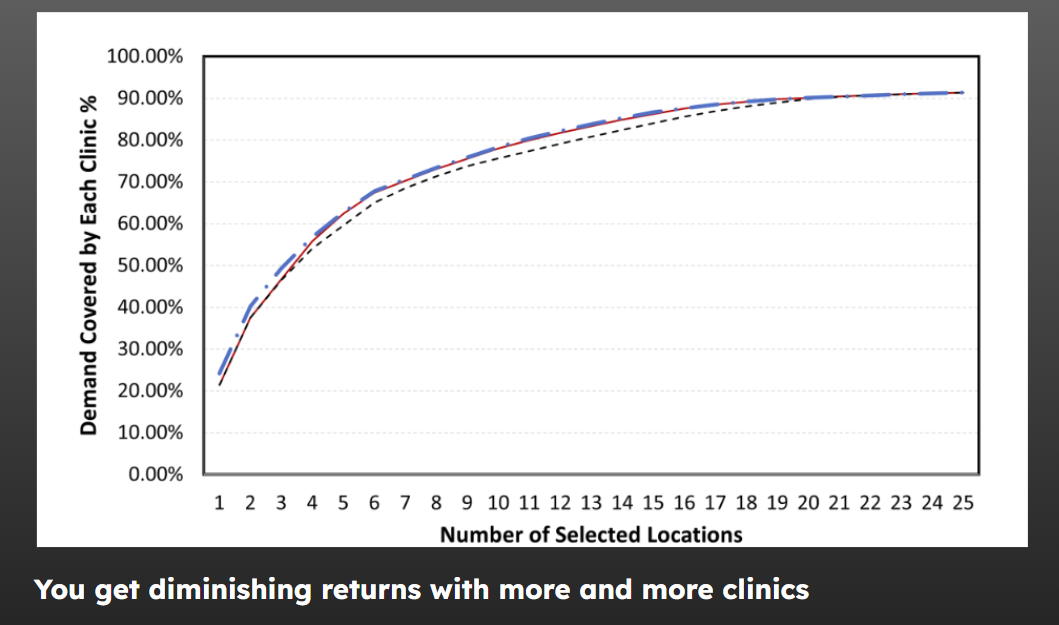
27.2 Formulating location allocation problems
27.2.1 Discrete vs continuous models
In discrete models, it is assumed that demands can be aggregated to a finite number of discrete points.
To achieve this, a region could be split up into a series of points (e.g. the central point of postcodes or LSOAs)
They also assume that there is a finite set of candidate locations where facilities will be placed.
The alternative is continuous models, where locations could be anywhere within a range - we don’t cover this!
27.2.2 Types of location allocation problem
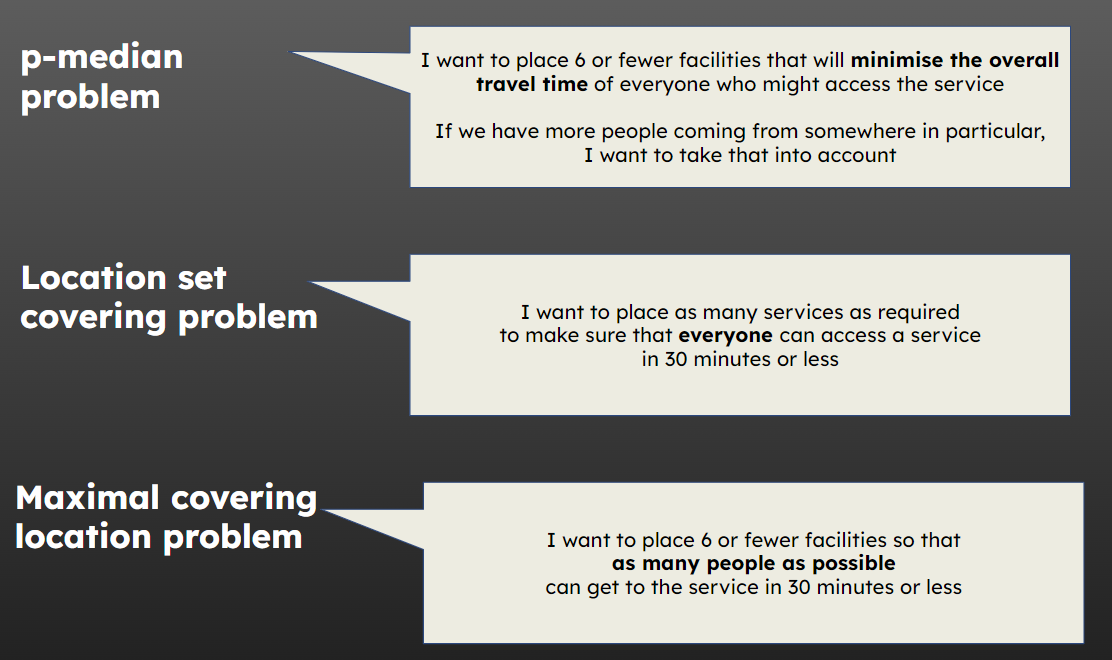

27.3 p-median problems
A p-median problem is basically just one where we care about
locating p services (so p could be 1, 2, 3, 5, 25 - whatever!)
in such a way that the weighted average travel time (or distance) of users is minimized
27.3.1 Understanding how p-median problems work
First, let’s imagine we have a single hospital site.
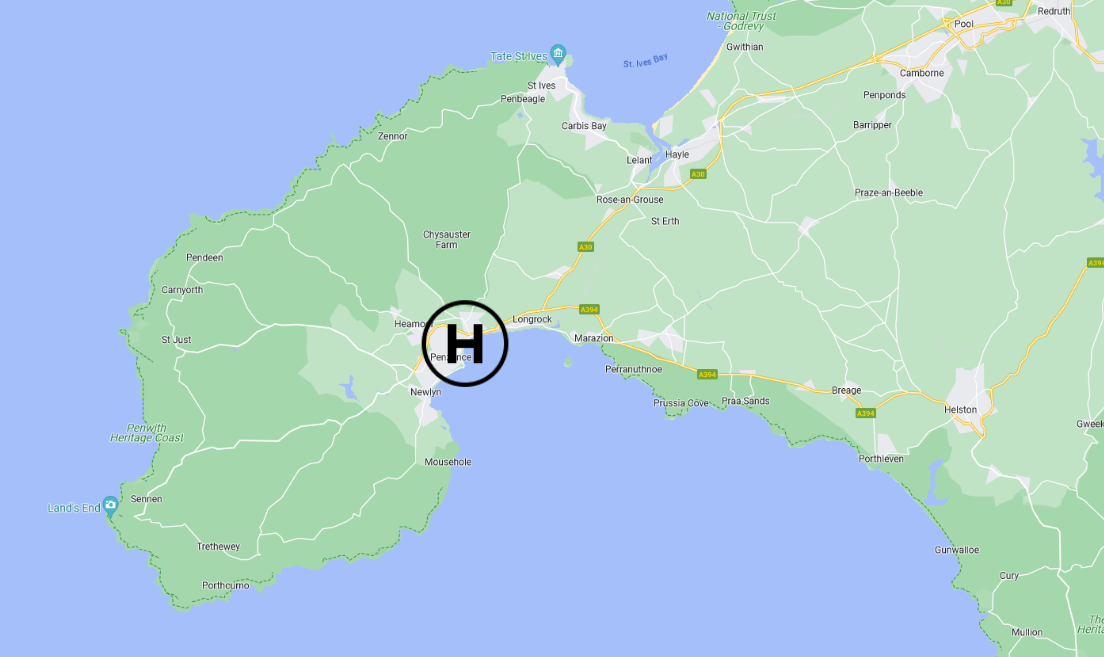
27.3.1.1 Simple averages
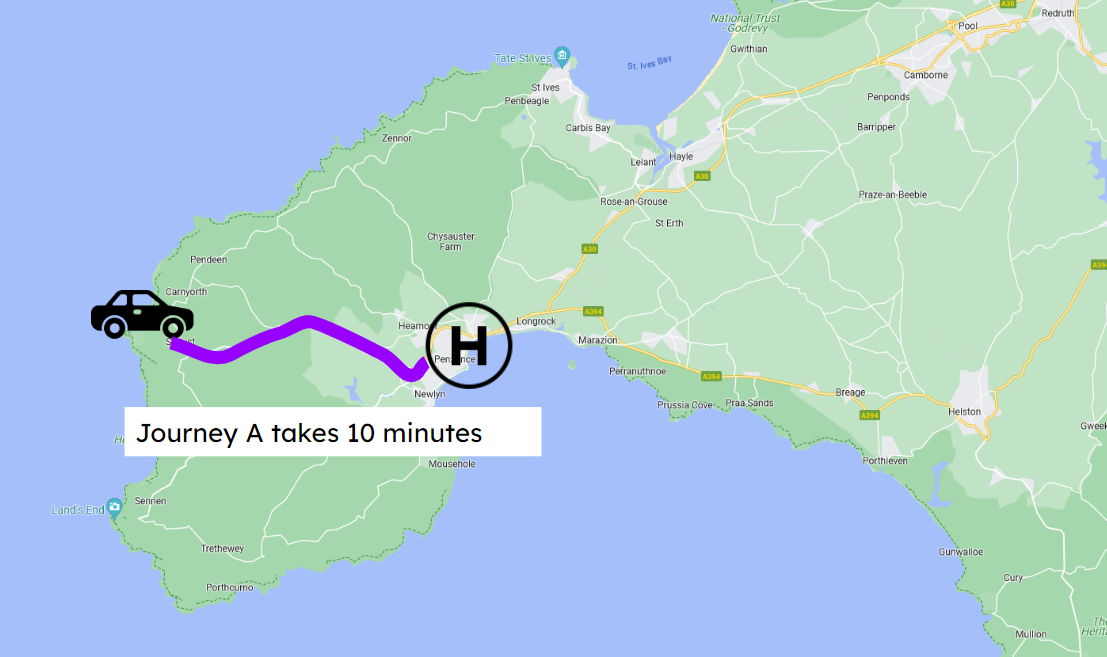
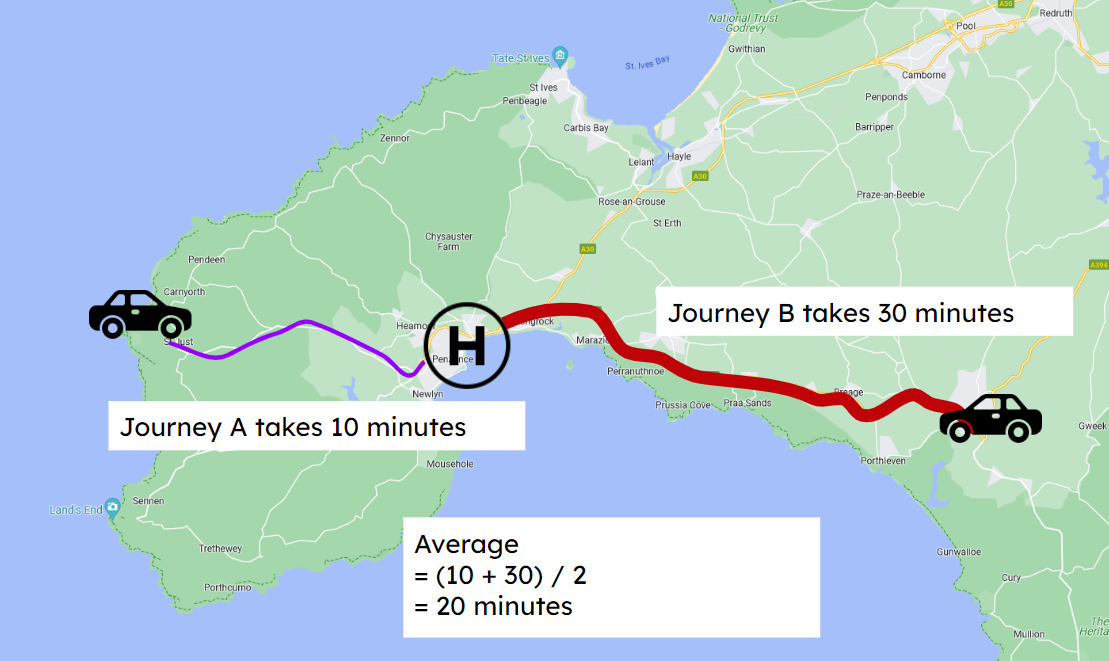
27.3.1.2 Why weighted averages?
27.3.1.3 Calculating weighted averages
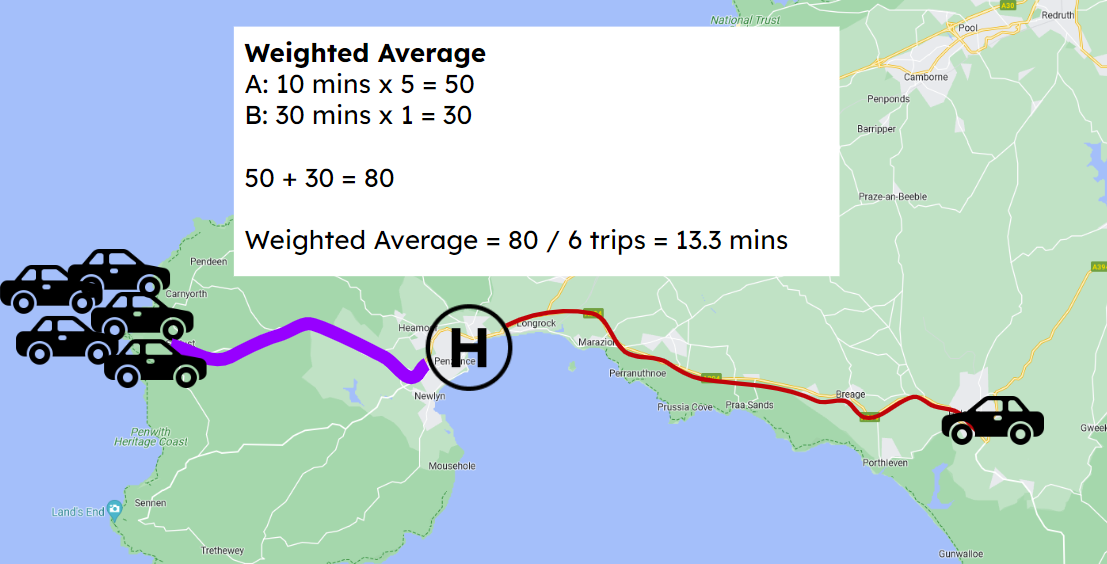
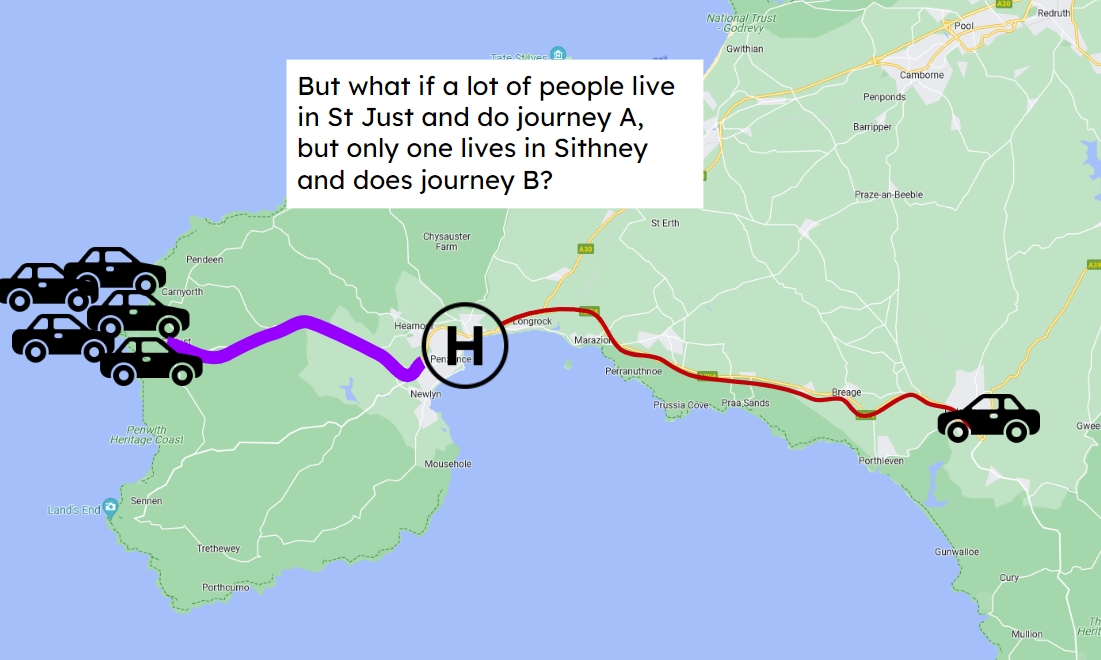
But what if the demand was distributed differently?
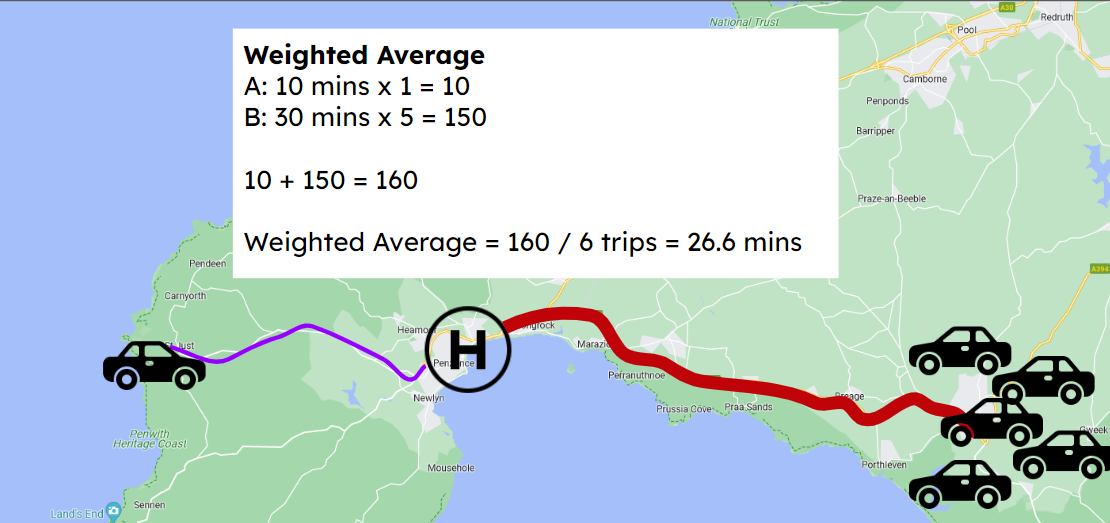
If this was the demand distribution instead, then this might not be such a good location for the hospital
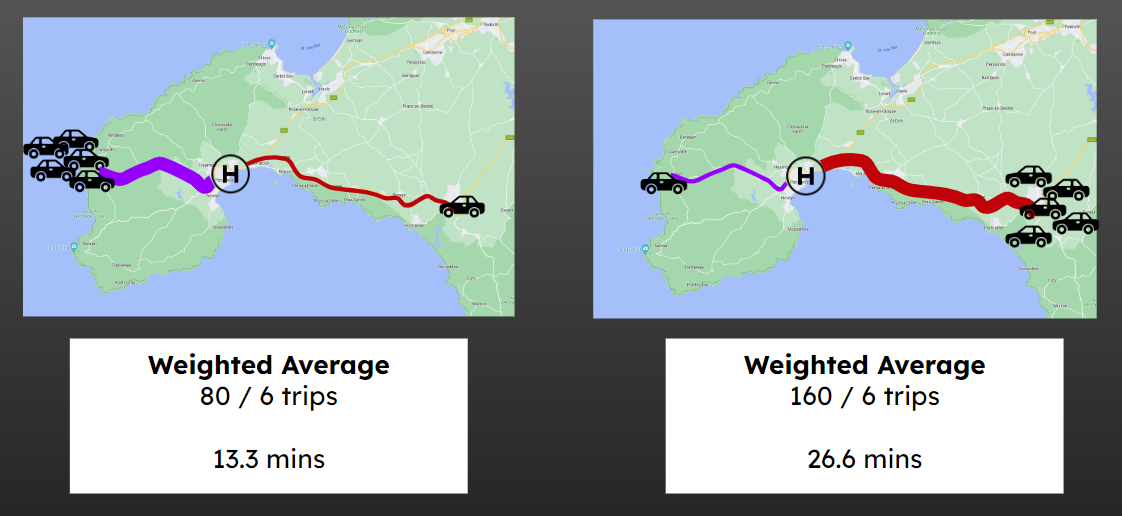
27.3.1.4 The impact of weighted averages
Compare our unweighted average

To the weighted averages
27.3.2 Limitations of p-median problems
However - one problem with this approach is that it doesn’t look at the maximum travel time.
For certain services, like accident and emergency, stroke units, or anything else where being able to get to a service within a certain length of time is crucial, then you may be less concerned about minimizing the average length.
Instead, you may care more about ensuring that everyone in your catchment area isn’t more than a certain number of miles or minutes away.
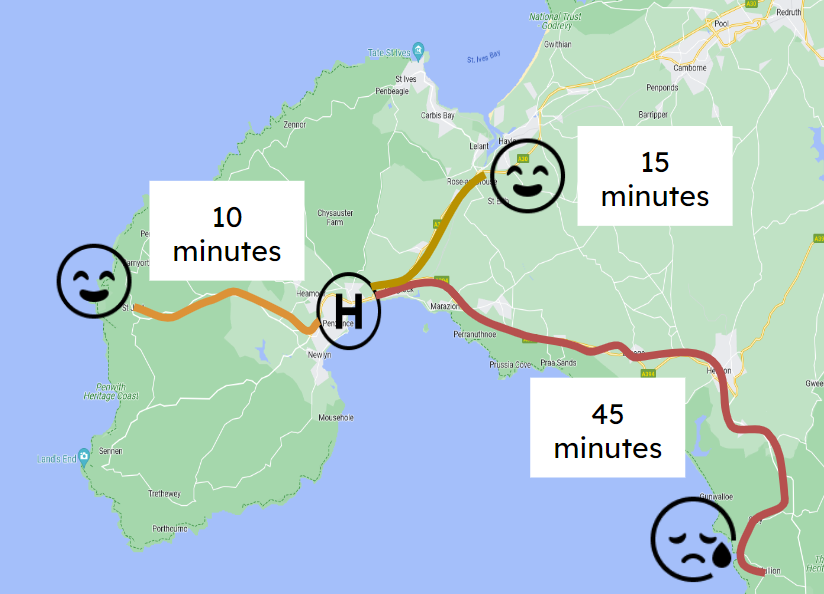
Just focussing on the weighted average time can lead to an inequitable solution.
27.4 Other problem types
We focus on the p-median problem in the course - but it’s useful to know what the other types are.
27.4.1 Location set covering problem
What is the minimum number of facilities (and their locations) so that all people have at least one facility within a given maximum distance (or time)
27.4.2 Maximal covering location problem
How can we locate the facilities in such a way that as few people as possible don’t have a service within the target distance (or time)
If we cannot cover all demands because it’s too expensive to do so, the model leans towards covering areas that generate lots of demand rather than those that generate less.
27.5 Presenting outputs
In reality, you might care about all of these to some extent!
You might find that your best solution to the p-median problem has a really long maximum travel time…
But your second best solution actually has a much more reasonable maximum travel time.
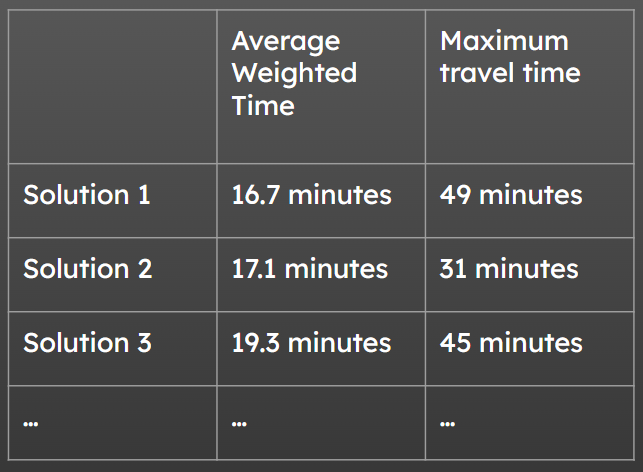
Make sure you’re not omitting this information when presenting the output to stakeholders!
It can be crucial to help them make an informed, fair and safe decision.
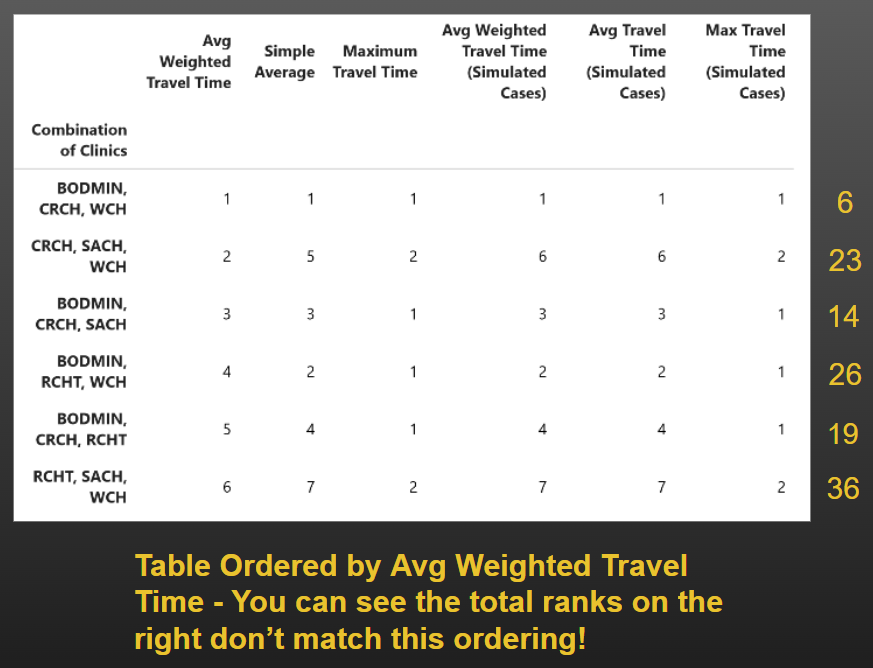
You could even consider ranking possible combinations by multiple methods and then seeing which has the lowest overall rank (indicating the best performance against multiple objectives)
27.6 References
Car icons created by fjstudio - Flaticon (https://www.flaticon.com/free-icons/car)
