28 Calculating combinations of sites
Much of the time, you will start with a series of known locations for services.
These will either be:
- Proposed locations for services
- Managers will often consider a range of possibilities based on buildings owned by the organisation, areas with buildings available for rent, and so on, before you receive a list of possibilities
- Alternatively, you can have more flexibility (e.g. allowing the centroid of each LSOA to be a possible location)
- Locations of existing services
- A mix of the two
You’ll also need a travel matrix, with
- the sources of demand (where people will be travelling from) as rows
- the destinations (all the possible clinic locations) as the columns travel times or distances as the values.
Sound familiar…?
Yep - that sounds like the travel matrices from the last section!
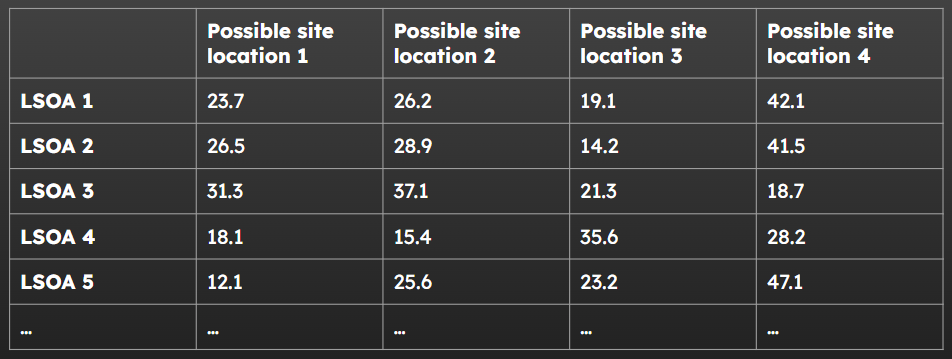
When we did our travel maps before, we just worked out the shortest possible distance
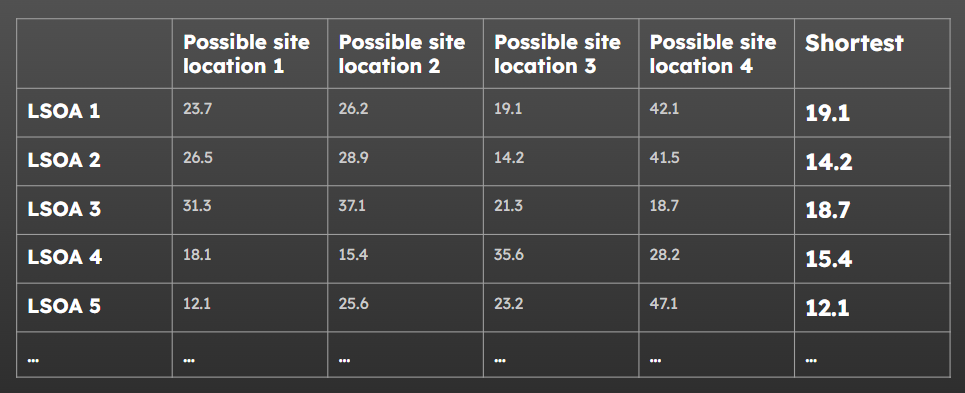
But now, we want to work out the shortest distance depending on which clinics are available
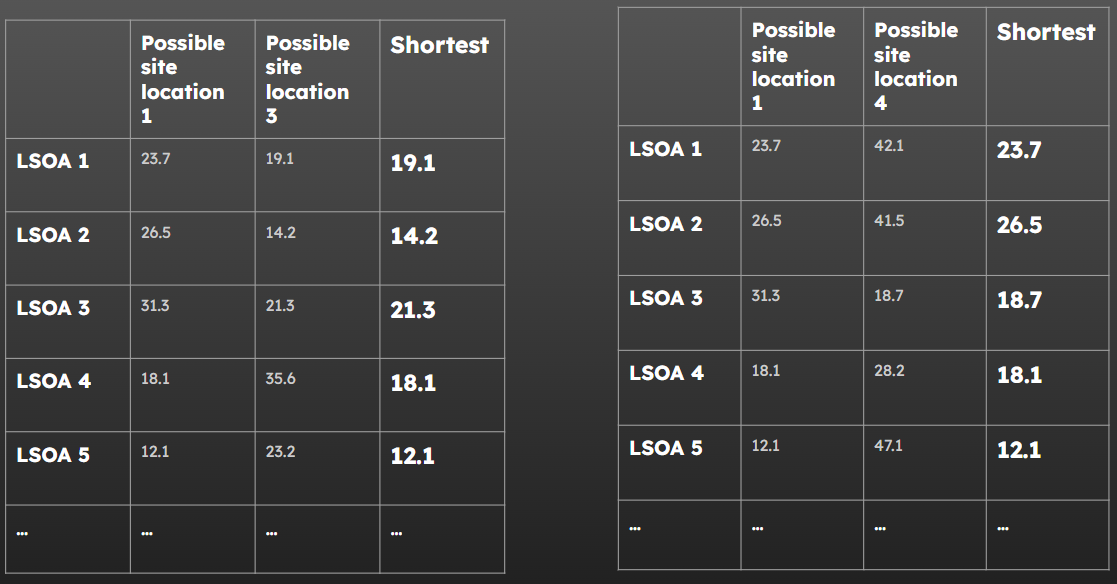
28.1 Representing possible combinations of sites
We then need to be able to represent these as an integer array
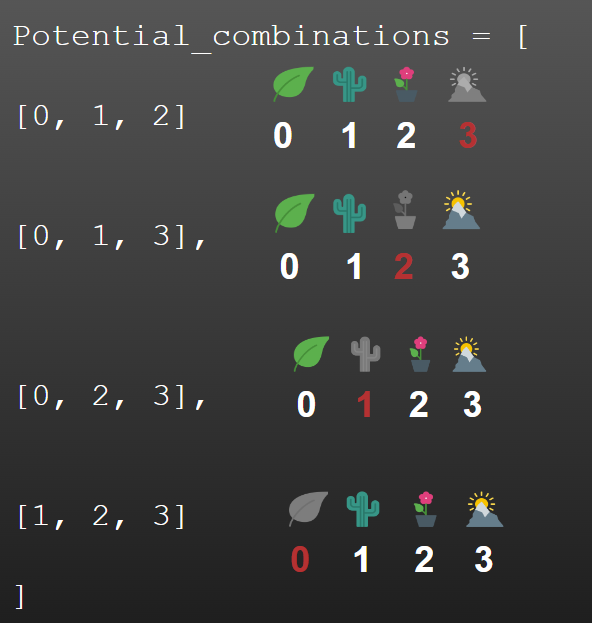
Let’s say we currently have four locations we deliver routine health screenings from.
Due to constraints, we’re going to have to cut it down to three.


28.1.1 Translating the problem for a computer

In our code, we will write this as a list of lists.
28.1.2 Using the itertools package for calculating combinations
And in fact, we won’t actually write it ourselves at all…
We’ll get the combinations function from the itertools package to do that for us - via a custom function.
n_facilities is the number of candidate locations where you could place facilities (e.g. clinics).
p is the number of clinics to place. This must be less than n_facilities.
This will return all possible combinations of clinic indices.
28.1.2.1 How is this function working?

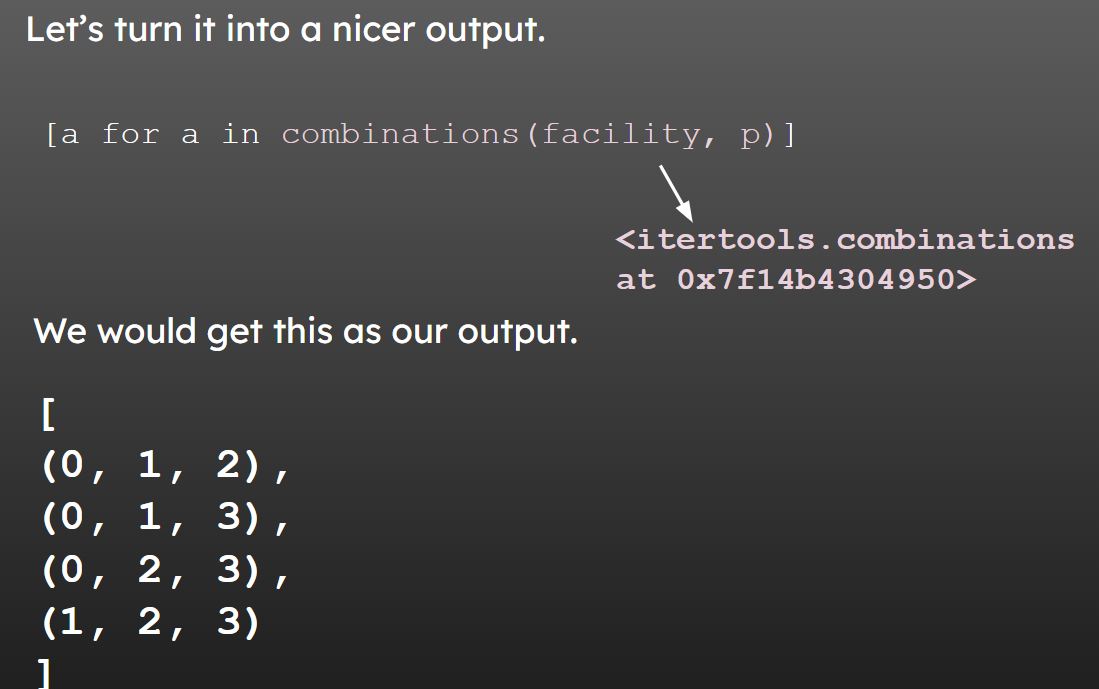

28.1.3 Larger problems
It turns out someone forgot to tell us about one of the practices!
But they are still just looking to drop it down to 3 practices.
So how many combinations can we get now?

Well, these are all of the possibilities.

Let’s add numeric indices to these for ease.

That was a bit of a pain to work out… so you can see why it’s really useful to have a function that will work this out for us when we get to bigger numbers of combinations!
But just how big can the number of combinations get?
28.2 Calculating the number of combinations
We can use the formula below to work out the total number of possible combinations in a scenario where the order of options doesn’t matter and you can’t repeat options in an answer.

The ! isn’t just emphasising things here.
It is the mathematical symbol for factorial.
So if we have 5 options, the top of our fraction is 5!, or 5 factorial.
This is 5 x 4 x 3 x 2 x 1
2! = 2 x 1
3! = 3 x 2 x 1
10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1

28.3 Limitations of brute-force problems
The key thing to note is that the number of combinations can get out of hand very quickly…
If you’re working at the level of a single trust, or with some fairly centralised services for an ICB, you’ll probably be ok.




There are ways to deal with situations where there are too many possibilities to ‘brute force’ - but it’s quite a tricky area to wrap your head around!
We’ll briefly cover this concept a bit later today, but we won’t cover how to do it in code or go into much detail about the process.
However, - we will link additional materials if you want to dive into this further - there are some members of the HSMA community with experience in this area if this is a route you need to go down for your HSMA project
28.4 References
Icons created by Pixel perfect - Flaticon: https://www.flaticon.com/packs/nature-46
