10  Exercise Solution: Regression with Trees (LOS Dataset)

If using colab, run this cell first. Otherwise, skip this cell.

!pip install ydata_profiling
!pip install catboost
!pip install --upgrade scikit-learn
!git clone https://github.com/hsma-programme/h6_4e_boosted_trees.git
%cd /content/h6_4e_boosted_trees/exercises_colab

10.1 Core

We’re going to work with a dataset to try to predict patient length of stay.

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

# import the relevant models from Sklearn, XGBoost, CatBoost and LightGBM
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from ydata_profiling import ProfileReport

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
from catboost import CatBoostRegressor
from sklearn.ensemble import HistGradientBoostingRegressor
# import any other libraries you need
import numpy as np
from sklearn.metrics import mean_absolute_error, mean_absolute_percentage_error, \
                            r2_score, root_mean_squared_error

Open the data dictionary in the los_dataset folder and take a look at what data is available.

Next, load in the dataframe containing the LOS data.

los_df = pd.read_csv("../datasets/los_dataset/LengthOfStay.csv", index_col="eid")

View the dataframe.

los_df.head()

	vdate	rcount	gender	dialysisrenalendstage	asthma	irondef	pneum	substancedependence	psychologicaldisordermajor	depress	...	sodium	glucose	bloodureanitro	creatinine	bmi	pulse	respiration	secondarydiagnosisnonicd9	facid	lengthofstay
eid
1	8/29/2012	0	F	0	0	0	0	0	0	0	...	140.361132	192.476918	12.0	1.390722	30.432418	96	6.5	4	B	3
2	5/26/2012	5+	F	0	0	0	0	0	0	0	...	136.731692	94.078507	8.0	0.943164	28.460516	61	6.5	1	A	7
3	9/22/2012	1	F	0	0	0	0	0	0	0	...	133.058514	130.530524	12.0	1.065750	28.843812	64	6.5	2	B	3
4	8/9/2012	0	F	0	0	0	0	0	0	0	...	138.994023	163.377028	12.0	0.906862	27.959007	76	6.5	1	A	1
5	12/20/2012	0	F	0	0	0	1	0	1	0	...	138.634836	94.886654	11.5	1.242854	30.258927	67	5.6	2	E	4

5 rows × 26 columns

ProfileReport(los_df)

Consider what columns to remove.

HINT: Is there a column in the dataset that doesn’t really make much sense to predict from? If you’re not sure, use the full dataset for now and come back to this later.

NOTE: For now, we’re going to assume that all of the included measures will be available to us at the point we need to make a prediction - they’re not things that will be calculated later in the patient’s stay.

los_df = los_df.drop(columns="vdate")
los_df.head(1)

	rcount	gender	dialysisrenalendstage	asthma	irondef	pneum	substancedependence	psychologicaldisordermajor	depress	psychother	...	sodium	glucose	bloodureanitro	creatinine	bmi	pulse	respiration	secondarydiagnosisnonicd9	facid	lengthofstay
eid
1	0	F	0	0	0	0	0	0	0	0	...	140.361132	192.476918	12.0	1.390722	30.432418	96	6.5	4	B	3

1 rows × 25 columns

Convert categories with only two options into a boolean value (e.g. for a gender column in which gender has only been provided as M or F, you could encode M as 0 and F as 1).

los_df.gender.unique()

array(['F', 'M'], dtype=object)

los_df['gender'].replace('M', 0, inplace=True)
los_df['gender'].replace('F', 1, inplace=True)

los_df.gender.unique()

array([1, 0], dtype=int64)

Convert columns with multiple options per category into multiple columns using one-hot encoding.

los_df.facid.unique()

# Bonus - astype('int') will convert the true/false values to 0/1
# not necessary - it will work regardless
one_hot = pd.get_dummies(los_df['facid']).astype('int')
los_df = los_df.drop('facid', axis=1)
los_df = los_df.join(one_hot)

los_df.head()

	rcount	gender	dialysisrenalendstage	asthma	irondef	pneum	substancedependence	psychologicaldisordermajor	depress	psychother	...	bmi	pulse	respiration	secondarydiagnosisnonicd9	lengthofstay	A	B	C	D	E
eid
1	0	1	0	0	0	0	0	0	0	0	...	30.432418	96	6.5	4	3	0	1	0	0	0
2	5+	1	0	0	0	0	0	0	0	0	...	28.460516	61	6.5	1	7	1	0	0	0	0
3	1	1	0	0	0	0	0	0	0	0	...	28.843812	64	6.5	2	3	0	1	0	0	0
4	0	1	0	0	0	0	0	0	0	0	...	27.959007	76	6.5	1	1	1	0	0	0	0
5	0	1	0	0	0	1	0	1	0	0	...	30.258927	67	5.6	2	4	0	0	0	0	1

5 rows × 29 columns

los_df.rcount.value_counts()

# Bonus - astype('int') will convert the true/false values to 0/1
# not necessary - it will work regardless
one_hot = pd.get_dummies(los_df['rcount'], prefix="rcount").astype('int')
los_df = los_df.drop('rcount', axis=1)
los_df = los_df.join(one_hot)
los_df.head()

	gender	dialysisrenalendstage	asthma	irondef	pneum	substancedependence	psychologicaldisordermajor	depress	psychother	fibrosisandother	...	B	C	D	E	rcount_0	rcount_1	rcount_2	rcount_3	rcount_4	rcount_5+
eid
1	1	0	0	0	0	0	0	0	0	0	...	1	0	0	0	1	0	0	0	0	0
2	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	1
3	1	0	0	0	0	0	0	0	0	0	...	1	0	0	0	0	1	0	0	0	0
4	1	0	0	0	0	0	0	0	0	0	...	0	0	0	0	1	0	0	0	0	0
5	1	0	0	0	1	0	1	0	0	0	...	0	0	0	1	1	0	0	0	0	0

5 rows × 34 columns

Train a decision tree model to predict length of stay based on the variables in this dataset.

X = los_df.drop(columns='lengthofstay')
y = los_df['lengthofstay']

X_train, X_test, y_train, y_test = train_test_split(
    X, y,
    test_size = 0.25,
    random_state=42
    )

regr_dt = DecisionTreeRegressor(random_state=42)

# Train the model using the training sets
regr_dt.fit(X_train, y_train)

# Make predictions using the testing set
y_pred_train = regr_dt.predict(X_train)
y_pred_test = regr_dt.predict(X_test)

y_pred_test

array([3., 1., 3., ..., 8., 2., 5.])

Assess the performance of this model.

print("TRAINING DATA")
print(f"Mean absolute error: {mean_absolute_error(y_train, y_pred_train):.2f}")
print(f"Mean absolute percentage error: {mean_absolute_percentage_error(y_train, y_pred_train):.2%}" )
print("Root Mean squared error: %.2f" % root_mean_squared_error(y_train, y_pred_train))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(y_train, y_pred_train))

TRAINING DATA
Mean absolute error: 0.00
Mean absolute percentage error: 0.00%
Root Mean squared error: 0.00
Coefficient of determination: 1.00

print("TESTING DATA")
print(f"Mean absolute error: {mean_absolute_error(y_test, y_pred_test):.2f}")
print(f"Mean absolute percentage error: {mean_absolute_percentage_error(y_test, y_pred_test):.2%}" )
print("Root Mean squared error: %.2f" % root_mean_squared_error(y_test, y_pred_test))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred_test))

TRAINING DATA
Mean absolute error: 0.50
Mean absolute percentage error: 12.94%
Root Mean squared error: 0.93
Coefficient of determination: 0.84

def plot_residuals(actual, predicted):
    residuals = actual - predicted

    plt.figure(figsize=(10, 5))
    plt.hist(residuals, bins=20)
    plt.axvline(x = 0, color = 'r')
    plt.xlabel('Residual')
    plt.ylabel('Frequency')
    plt.title('Distribution of Residuals')
    plt.show()

plot_residuals(y_test, y_pred_test)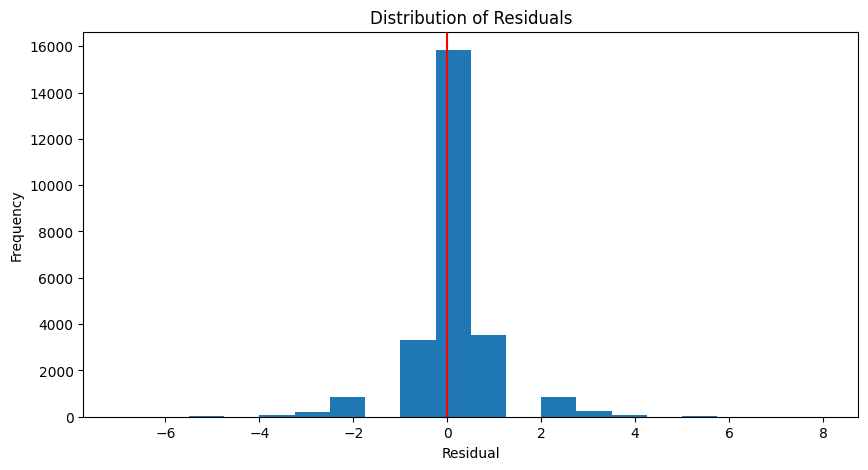

Note that here the alpha parameter has been set to 0.05 - this means that the points will be transparent. Higher numbers of points in a given space will appear more opaque.

def plot_actual_vs_predicted(actual, predicted):
    fig, ax = plt.subplots(figsize=(6, 6))

    ax.scatter(actual, predicted, color="black", alpha=0.05)
    ax.axline((1, 1), slope=1)
    plt.xlabel('True Values')
    plt.ylabel('Predicted Values')
    plt.title('True vs Predicted Values')
    plt.show()

plot_actual_vs_predicted(y_test, y_pred_test)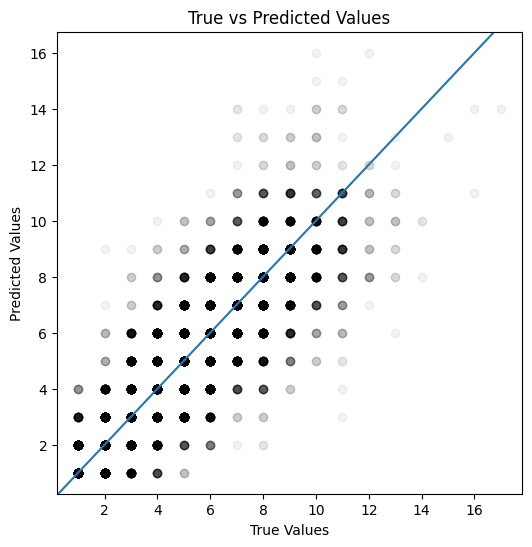

Train a boosting model to predict length of stay based on the variables in this dataset.

X = los_df.drop(columns='lengthofstay')
y = los_df['lengthofstay']

X_train, X_test, y_train, y_test = train_test_split(
    X, y,
    test_size = 0.25,
    random_state=42
    )

regr_xgb = XGBRegressor(random_state=42)

# Train the model using the training sets
regr_xgb.fit(X_train, y_train)

# Make predictions using the testing set
y_pred_train = regr_xgb.predict(X_train)
y_pred_test = regr_xgb.predict(X_test)

y_pred_test

array([3.6313417, 0.8304186, 2.4800673, ..., 5.5354204, 1.5881324,
       5.249632 ], dtype=float32)

Assess the performance of this model and compare it with your decision tree model.

print("TRAINING DATA")
print(f"Mean absolute error: {mean_absolute_error(y_train, y_pred_train):.2f}")
print(f"Mean absolute percentage error: {mean_absolute_percentage_error(y_train, y_pred_train):.2%}" )
print("Root Mean squared error: %.2f" % root_mean_squared_error(y_train, y_pred_train))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(y_train, y_pred_train))

TRAINING DATA
Mean absolute error: 0.29
Mean absolute percentage error: 10.66%
Root Mean squared error: 0.37
Coefficient of determination: 0.98

print("TESTING DATA")
print(f"Mean absolute error: {mean_absolute_error(y_test, y_pred_test):.2f}")
print(f"Mean absolute percentage error: {mean_absolute_percentage_error(y_test, y_pred_test):.2%}" )
print("Root Mean squared error: %.2f" % root_mean_squared_error(y_test, y_pred_test))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred_test))

TESTING DATA
Mean absolute error: 0.33
Mean absolute percentage error: 11.60%
Root Mean squared error: 0.44
Coefficient of determination: 0.96

plot_residuals(y_test, y_pred_test)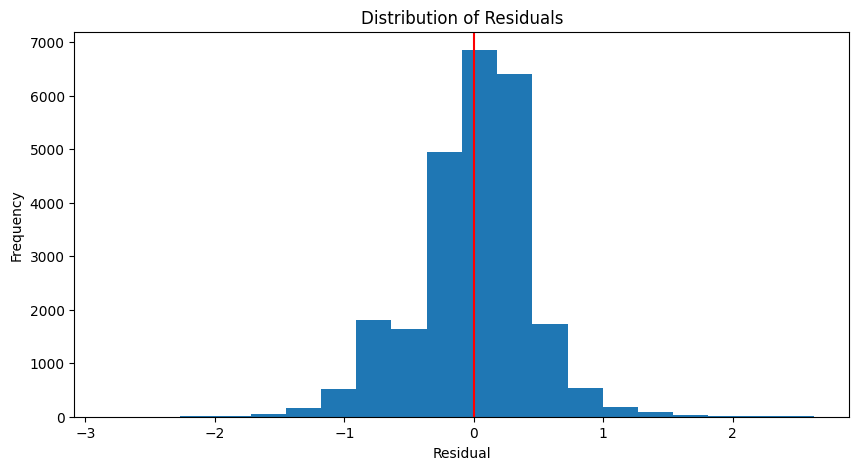

plot_actual_vs_predicted(y_test, y_pred_test)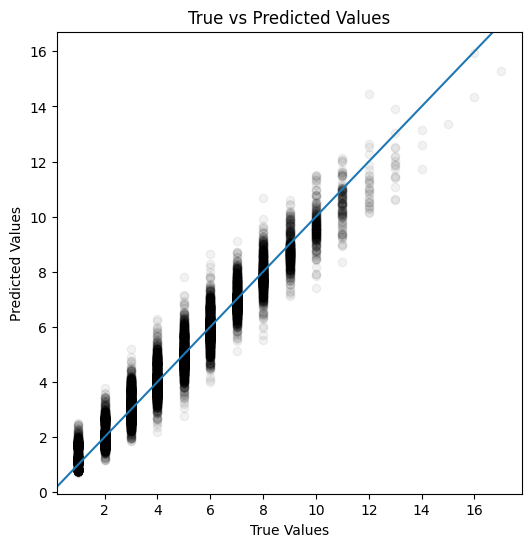

10.2 Extension

Continue to refine your model.

You could - tune hyperparameters - try additional model types (e.g. different boosting trees, linear regression) - try dropping some features - calculate additional metrics - add some visualisations of the features in the dataset - store the results from your different model iterations and display this as a table of metrics - turn this table of metrics into a graph - try using k-fold cross validation

# NO SOLUTION GIVEN

11 Challenge

Explore additional aspects of regression modelling using Google, sklearn and other library documentation, Stack Overflow, AI tools, or other avenues.

Some suggestions to get you started: - Look up the assumptions of linear regression. Would our dataset violate any of these assumptions? - What about multiple linear regression? - Investigate the performance of your model on different subsets of the data. Are the errors lower for male and female patients? How about across the different facilities?

# NO SOLUTION GIVEN