# Class to store global parameter values. We don't create an instance of this
# class - we just refer to the class blueprint itself to access the numbers
# inside.
class g:
patient_inter = 5
mean_reception_time = 2
mean_n_consult_time = 6
mean_d_consult_time = 20 ##NEW
number_of_receptionists = 1
number_of_nurses = 1
number_of_doctors = 2 ##NEW
prob_seeing_doctor = 0.6 ##NEW
sim_duration = 120
number_of_runs = 57 Adding Branching Paths
“Most real world systems aren’t linear!” we hear you say. “Some people go over here, some go over there.”
You want branching paths? Coming right up!
So this time, instead of this model

Or this model

We will create something more like this:
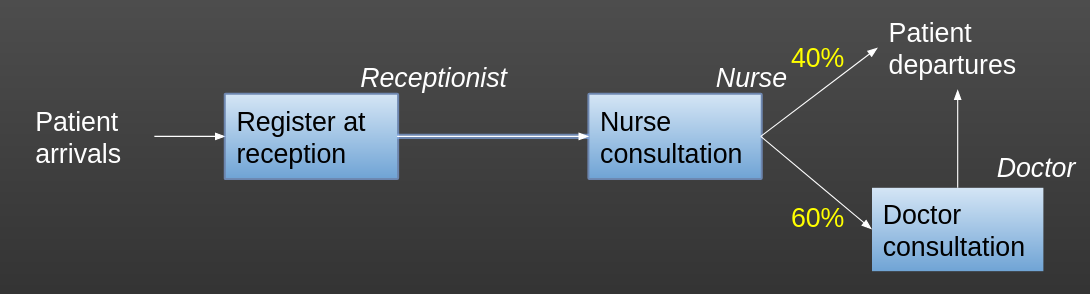
To model a branching path, we can use our good old Python friend Conditional Logic.
Often, the branches in a DES are based on probabilities that represent the proportion of patients (or whatever your entity is) that travel along a certain route. For example, the data might show that 60% of patients see a doctor after seeing a nurse.
To model this, we can randomly sample from a uniform distribution between 0 and 1, and compare the value to this probability. If we pick a value below the probability, then we say that the patient follows this route. Why does this work? Well…

60% of values between 0 and 1 are below 0.6.
Therefore, if there’s an equal chance of any value being picked (as is the case in a uniform distribution) then there’s a 60% probability of picking one below 0.6.
We can use this to emulate the probability of following a path.
Not all branching paths will be probability-based.
It may be that some paths are followed depending on - the time of day - the type of patient - how long a patient spends in an activity - etc.
In these cases, you’d still use conditional logic, but just alter the condition you’re checking.
For the time of day, you’d want to check the current simulation time in the run.
For the type of patient, you may have stored this in an attribute of the patient.
Throughout the code, anything new that’s been added will be followed by the comment ##NEW - so look out for that in the following code chunks.
7.1 Coding the model
7.1.1 the g class
We need to add a few additional parameters to our g class.
7.1.2 The Patient class
We want to add an additional attribute to record the time patients spend with the doctor if they see one.
# Class representing patients coming in to the clinic.
class Patient:
def __init__(self, p_id):
self.id = p_id
self.q_time_recep = 0
self.q_time_nurse = 0
self.q_time_doctor = 0 ##NEW7.1.3 The model class
7.1.3.1 the init method
In the init method, we add a few additional atrributes to store additional outputs from the model.
# Class representing our model of the clinic.
class Model:
# Constructor to set up the model for a run. We pass in a run number when
# we create a new model.
def __init__(self, run_number):
# Create a SimPy environment in which everything will live
self.env = simpy.Environment()
# Create a patient counter (which we'll use as a patient ID)
self.patient_counter = 0
# Create our resources
self.receptionist = simpy.Resource(
self.env, capacity=g.number_of_receptionists
)
self.nurse = simpy.Resource(self.env, capacity=g.number_of_nurses)
self.doctor = simpy.Resource(
self.env, capacity=g.number_of_doctors) ##NEW
# Store the passed in run number
self.run_number = run_number
# Create a new Pandas DataFrame that will store some results against
# the patient ID (which we'll use as the index).
self.results_df = pd.DataFrame()
self.results_df["Patient ID"] = [1]
self.results_df["Q Time Recep"] = [0.0]
self.results_df["Time with Recep"] = [0.0]
self.results_df["Q Time Nurse"] = [0.0]
self.results_df["Time with Nurse"] = [0.0]
self.results_df["Q Time Doctor"] = [0.0] ##NEW
self.results_df["Time with Doctor"] = [0.0] ##NEW
self.results_df.set_index("Patient ID", inplace=True)
# Create an attribute to store the mean queuing times across this run of
# the model
self.mean_q_time_recep = 0
self.mean_q_time_nurse = 0
self.mean_q_time_doctor = 0 ##NEW7.1.3.2 The generator_patient_arrivals method
This method is unchanged.
7.1.3.3 The attend_clinic method
Here, we need to add in a chance of patients seeing the doctor on their journey.
def attend_clinic(self, patient):
start_q_recep = self.env.now
with self.receptionist.request() as req:
yield req
end_q_recep = self.env.now
patient.q_time_recep = end_q_recep - start_q_recep
sampled_recep_act_time = random.expovariate(
1.0 / g.mean_reception_time
)
self.results_df.at[patient.id, "Q Time Recep"] = (
patient.q_time_recep
)
self.results_df.at[patient.id, "Time with Recep"] = (
sampled_recep_act_time
)
yield self.env.timeout(sampled_recep_act_time)
# Here's where the patient finishes with the receptionist, and starts
# queuing for the nurse
start_q_nurse = self.env.now
with self.nurse.request() as req:
yield req
end_q_nurse = self.env.now
patient.q_time_nurse = end_q_nurse - start_q_nurse
sampled_nurse_act_time = random.expovariate(1.0 /
g.mean_n_consult_time)
self.results_df.at[patient.id, "Q Time Nurse"] = (
patient.q_time_nurse)
self.results_df.at[patient.id, "Time with Nurse"] = (
sampled_nurse_act_time)
yield self.env.timeout(sampled_nurse_act_time)
# When the time above elapses, the generator function will return
# here. As there's nothing more that we've written, the function
# will simply end. This is a sink.
##NEW
##
## -----------------------------------------------------------
## This is where our new code for seeing the doctor is
## We use conditional logic to determine whether the patient goes
## on to see the doctor or not
## ------------------------------------------------------------
#
# We sample from the uniform distribution between 0 and 1. If the value
# is less than the probability of seeing a doctor (stored in g Class)
# then we say the patient sees a doctor.
#
# If not, this block of code won't be run and the patient will just
# leave the system (we could add in an else if we wanted a branching
# path to another activity instead)
if random.uniform(0,1) < g.prob_seeing_doctor:
start_q_doctor = self.env.now
with self.doctor.request() as req:
yield req
end_q_doctor = self.env.now
patient.q_time_doctor = end_q_doctor - start_q_doctor
sampled_doctor_act_time = random.expovariate(
1.0 / g.mean_d_consult_time
)
self.results_df.at[patient.id, "Q Time Doctor"] = (
patient.q_time_doctor
)
self.results_df.at[patient.id, "Time with Doctor"] = (
sampled_doctor_act_time
)
yield self.env.timeout(sampled_doctor_act_time)Let’s try and understand a bit more about how we trigger the conditional logic.
Let’s look at the output of the line random.uniform(0,1)
random.uniform(0,1)0.6394267984578837What about if we run it multiple times?
for i in range(10):
print(random.uniform(0,1))0.025010755222666936
0.27502931836911926
0.22321073814882275
0.7364712141640124
0.6766994874229113
0.8921795677048454
0.08693883262941615
0.4219218196852704
0.029797219438070344
0.21863797480360336So how does this relate to our code?
In our g class, we set a probability threshold for patients being seen. Let’s pull that out:
print(g.prob_seeing_doctor)0.6The code in the Model class tests whether the number generated by the random number generator is below the threshold we’ve set of seeing the doctor. If it is, the indented code where we actually see the doctor will be run for that patient. If it is not, that bit is bypassed - which in this case means they’ve reached the end of their journey and leave the system (a sink).
for i in range(10):
random_number = random.uniform(0,1)
is_below_threshold = random_number < g.prob_seeing_doctor
if is_below_threshold:
print(f"Random number {random_number:.2f} is LOWER than threshold ({g.prob_seeing_doctor}). " +
"Doctor code is triggered.")
else:
print(f"Random number {random_number:.2f} is HIGHER than threshold ({g.prob_seeing_doctor}). " +
"Doctor code is **not** triggered.")Random number 0.51 is LOWER than threshold (0.6). Doctor code is triggered.
Random number 0.03 is LOWER than threshold (0.6). Doctor code is triggered.
Random number 0.20 is LOWER than threshold (0.6). Doctor code is triggered.
Random number 0.65 is HIGHER than threshold (0.6). Doctor code is **not** triggered.
Random number 0.54 is LOWER than threshold (0.6). Doctor code is triggered.
Random number 0.22 is LOWER than threshold (0.6). Doctor code is triggered.
Random number 0.59 is LOWER than threshold (0.6). Doctor code is triggered.
Random number 0.81 is HIGHER than threshold (0.6). Doctor code is **not** triggered.
Random number 0.01 is LOWER than threshold (0.6). Doctor code is triggered.
Random number 0.81 is HIGHER than threshold (0.6). Doctor code is **not** triggered.If we run this code a hundred thousand times and plot the results, we can start to see the pattern emerging despite the random element of the number generator.
import plotly.express as px
import pandas as pd
import numpy as np
random_vals = [random.uniform(0,1) for i in range(100000)]
random_vals_df = pd.DataFrame({"value" :random_vals})
random_vals_df['threshold'] = np.where(random_vals_df["value"]<0.6, 'below', 'above')
fig = px.histogram(random_vals_df, color="threshold")
fig.update_traces(xbins=dict(
start=0.0,
end=1.0,
size=0.1
),
marker_line_width=1,marker_line_color="black")
fig.show()So for every 1000 patients, roughly 600 will see a doctor, and roughly 400 will leave the system straight after seeing the nurse.
7.1.3.4 The calculate_run_results method
In this method, we just add an additional step to measure the mean time spent queueing for a doctor across all patients in this run.
# This method calculates results over a single run. Here we just calculate
# a mean, but in real world models you'd probably want to calculate more.
def calculate_run_results(self):
# Take the mean of the queuing times across patients in this run of the
# model.
self.mean_q_time_recep = self.results_df["Q Time Recep"].mean()
self.mean_q_time_nurse = self.results_df["Q Time Nurse"].mean()
self.mean_q_time_doctor = self.results_df["Q Time Doctor"].mean() ##NEW7.1.3.5 The run method
The run method is unchanged
7.1.4 The trial class
7.1.4.1 The init method
In the init method, we just add a placeholder for measuring the mean queue time of a doctor.
def __init__(self):
self.df_trial_results = pd.DataFrame()
self.df_trial_results["Run Number"] = [0]
self.df_trial_results["Mean Q Time Recep"] = [0.0]
self.df_trial_results["Mean Q Time Nurse"] = [0.0]
self.df_trial_results["Mean Q Time Doctor"] = [0.0] ##NEW
self.df_trial_results.set_index("Run Number", inplace=True)7.1.4.2 The run_trial method
Here, we just add in the mean queue time for the doctor to the trial results dataframe.
def run_trial(self):
# Run the simulation for the number of runs specified in g class.
# For each run, we create a new instance of the Model class and call its
# run method, which sets everything else in motion. Once the run has
# completed, we grab out the stored run results (just mean queuing time
# here) and store it against the run number in the trial results
# dataframe.
for run in range(g.number_of_runs):
my_model = Model(run)
my_model.run()
##NEW - added mean queue time for doctor to end of list
self.df_trial_results.loc[run] = [my_model.mean_q_time_recep,
my_model.mean_q_time_nurse,
my_model.mean_q_time_doctor]
# Once the trial (ie all runs) has completed, print the final results
self.print_trial_results()7.2 Evaluating the outputs
Below is the full updated code for this model.
import simpy
import random
import pandas as pd
# Class to store global parameter values. We don't create an instance of this
# class - we just refer to the class blueprint itself to access the numbers
# inside.
class g:
patient_inter = 5
mean_reception_time = 2
mean_n_consult_time = 6
mean_d_consult_time = 20 ##NEW
number_of_receptionists = 1
number_of_nurses = 1
number_of_doctors = 2 ##NEW
prob_seeing_doctor = 0.6 ##NEW
sim_duration = 120
number_of_runs = 1
# Class representing patients coming in to the clinic.
class Patient:
def __init__(self, p_id):
self.id = p_id
self.q_time_recep = 0
self.q_time_nurse = 0
self.q_time_doctor = 0 ##NEW
# Class representing our model of the clinic.
class Model:
# Constructor to set up the model for a run. We pass in a run number when
# we create a new model.
def __init__(self, run_number):
# Create a SimPy environment in which everything will live
self.env = simpy.Environment()
# Create a patient counter (which we'll use as a patient ID)
self.patient_counter = 0
# Create our resources
self.receptionist = simpy.Resource(
self.env, capacity=g.number_of_receptionists
)
self.nurse = simpy.Resource(self.env, capacity=g.number_of_nurses)
self.doctor = simpy.Resource(
self.env, capacity=g.number_of_doctors) ##NEW
# Store the passed in run number
self.run_number = run_number
# Create a new Pandas DataFrame that will store some results against
# the patient ID (which we'll use as the index).
self.results_df = pd.DataFrame()
self.results_df["Patient ID"] = [1]
self.results_df["Q Time Recep"] = [0.0]
self.results_df["Time with Recep"] = [0.0]
self.results_df["Q Time Nurse"] = [0.0]
self.results_df["Time with Nurse"] = [0.0]
self.results_df["Q Time Doctor"] = [0.0] ##NEW
self.results_df["Time with Doctor"] = [0.0] ##NEW
self.results_df.set_index("Patient ID", inplace=True)
# Create an attribute to store the mean queuing times across this run of
# the model
self.mean_q_time_recep = 0
self.mean_q_time_nurse = 0
self.mean_q_time_doctor = 0 ##NEW
# A generator function that represents the DES generator for patient
# arrivals
def generator_patient_arrivals(self):
# We use an infinite loop here to keep doing this indefinitely whilst
# the simulation runs
while True:
# Increment the patient counter by 1 (this means our first patient
# will have an ID of 1)
self.patient_counter += 1
# Create a new patient - an instance of the Patient Class we
# defined above. Remember, we pass in the ID when creating a
# patient - so here we pass the patient counter to use as the ID.
p = Patient(self.patient_counter)
# Tell SimPy to start up the attend_clinic generator function with
# this patient (the generator function that will model the
# patient's journey through the system)
self.env.process(self.attend_clinic(p))
# Randomly sample the time to the next patient arriving. Here, we
# sample from an exponential distribution (common for inter-arrival
# times), and pass in a lambda value of 1 / mean. The mean
# inter-arrival time is stored in the g class.
sampled_inter = random.expovariate(1.0 / g.patient_inter)
# Freeze this instance of this function in place until the
# inter-arrival time we sampled above has elapsed. Note - time in
# SimPy progresses in "Time Units", which can represent anything
# you like (just make sure you're consistent within the model)
yield self.env.timeout(sampled_inter)
# A generator function that represents the pathway for a patient going
# through the clinic.
# The patient object is passed in to the generator function so we can
# extract information from / record information to it
def attend_clinic(self, patient):
start_q_recep = self.env.now
with self.receptionist.request() as req:
yield req
end_q_recep = self.env.now
patient.q_time_recep = end_q_recep - start_q_recep
sampled_recep_act_time = random.expovariate(
1.0 / g.mean_reception_time
)
self.results_df.at[patient.id, "Q Time Recep"] = (
patient.q_time_recep
)
self.results_df.at[patient.id, "Time with Recep"] = (
sampled_recep_act_time
)
yield self.env.timeout(sampled_recep_act_time)
# Here's where the patient finishes with the receptionist, and starts
# queuing for the nurse
# Record the time the patient started queuing for a nurse
start_q_nurse = self.env.now
# This code says request a nurse resource, and do all of the following
# block of code with that nurse resource held in place (and therefore
# not usable by another patient)
with self.nurse.request() as req:
# Freeze the function until the request for a nurse can be met.
# The patient is currently queuing.
yield req
# When we get to this bit of code, control has been passed back to
# the generator function, and therefore the request for a nurse has
# been met. We now have the nurse, and have stopped queuing, so we
# can record the current time as the time we finished queuing.
end_q_nurse = self.env.now
# Calculate the time this patient was queuing for the nurse, and
# record it in the patient's attribute for this.
patient.q_time_nurse = end_q_nurse - start_q_nurse
# Now we'll randomly sample the time this patient with the nurse.
# Here, we use an Exponential distribution for simplicity, but you
# would typically use a Log Normal distribution for a real model
# (we'll come back to that). As with sampling the inter-arrival
# times, we grab the mean from the g class, and pass in 1 / mean
# as the lambda value.
sampled_nurse_act_time = random.expovariate(1.0 /
g.mean_n_consult_time)
# Here we'll store the queuing time for the nurse and the sampled
# time to spend with the nurse in the results DataFrame against the
# ID for this patient. In real world models, you may not want to
# bother storing the sampled activity times - but as this is a
# simple model, we'll do it here.
# We use a handy property of pandas called .at, which works a bit
# like .loc. .at allows us to access (and therefore change) a
# particular cell in our DataFrame by providing the row and column.
# Here, we specify the row as the patient ID (the index), and the
# column for the value we want to update for that patient.
self.results_df.at[patient.id, "Q Time Nurse"] = (
patient.q_time_nurse)
self.results_df.at[patient.id, "Time with Nurse"] = (
sampled_nurse_act_time)
# Freeze this function in place for the activity time we sampled
# above. This is the patient spending time with the nurse.
yield self.env.timeout(sampled_nurse_act_time)
# When the time above elapses, the generator function will return
# here. As there's nothing more that we've written, the function
# will simply end. This is a sink. We could choose to add
# something here if we wanted to record something - e.g. a counter
# for number of patients that left, recording something about the
# patients that left at a particular sink etc.
##NEW added conditional logic to see if patient goes on to see doctor
# We sample from the uniform distribution between 0 and 1. If the value
# is less than the probability of seeing a doctor (stored in g Class)
# then we say the patient sees a doctor.
# If not, this block of code won't be run and the patient will just
# leave the system (we could add in an else if we wanted a branching
# path to another activity instead)
if random.uniform(0,1) < g.prob_seeing_doctor:
start_q_doctor = self.env.now
with self.doctor.request() as req:
yield req
end_q_doctor = self.env.now
patient.q_time_doctor = end_q_doctor - start_q_doctor
sampled_doctor_act_time = random.expovariate(
1.0 / g.mean_d_consult_time
)
self.results_df.at[patient.id, "Q Time Doctor"] = (
patient.q_time_doctor
)
self.results_df.at[patient.id, "Time with Doctor"] = (
sampled_doctor_act_time
)
yield self.env.timeout(sampled_doctor_act_time)
# This method calculates results over a single run. Here we just calculate
# a mean, but in real world models you'd probably want to calculate more.
def calculate_run_results(self):
# Take the mean of the queuing times across patients in this run of the
# model.
self.mean_q_time_recep = self.results_df["Q Time Recep"].mean()
self.mean_q_time_nurse = self.results_df["Q Time Nurse"].mean()
self.mean_q_time_doctor = self.results_df["Q Time Doctor"].mean() ##NEW
# The run method starts up the DES entity generators, runs the simulation,
# and in turns calls anything we need to generate results for the run
def run(self):
# Start up our DES entity generators that create new patients. We've
# only got one in this model, but we'd need to do this for each one if
# we had multiple generators.
self.env.process(self.generator_patient_arrivals())
# Run the model for the duration specified in g class
self.env.run(until=g.sim_duration)
# Now the simulation run has finished, call the method that calculates
# run results
self.calculate_run_results()
# Print the run number with the patient-level results from this run of
# the model
print (f"Run Number {self.run_number}")
print (self.results_df)
# Class representing a Trial for our simulation - a batch of simulation runs.
class Trial:
# The constructor sets up a pandas dataframe that will store the key
# results from each run against run number, with run number as the index.
def __init__(self):
self.df_trial_results = pd.DataFrame()
self.df_trial_results["Run Number"] = [0]
self.df_trial_results["Mean Q Time Recep"] = [0.0]
self.df_trial_results["Mean Q Time Nurse"] = [0.0]
self.df_trial_results["Mean Q Time Doctor"] = [0.0] ##NEW
self.df_trial_results.set_index("Run Number", inplace=True)
# Method to print out the results from the trial. In real world models,
# you'd likely save them as well as (or instead of) printing them
def print_trial_results(self):
print ("Trial Results")
print (self.df_trial_results)
# Method to run a trial
def run_trial(self):
# Run the simulation for the number of runs specified in g class.
# For each run, we create a new instance of the Model class and call its
# run method, which sets everything else in motion. Once the run has
# completed, we grab out the stored run results (just mean queuing time
# here) and store it against the run number in the trial results
# dataframe.
for run in range(g.number_of_runs):
my_model = Model(run)
my_model.run()
##NEW - added mean queue time for doctor to end of list
self.df_trial_results.loc[run] = [my_model.mean_q_time_recep,
my_model.mean_q_time_nurse,
my_model.mean_q_time_doctor]
# Once the trial (ie all runs) has completed, print the final results
self.print_trial_results()Let’s look at the outputs for a single run.
When a patient doesn’t see a doctor, notice that their value for that row is NaN - which stands for “not a number”. This will be treated differently to 0 in calculations of the mean - i.e. it won’t be included at all, whereas a queue time of 0 will matter.
# Create an instance of the Trial class
my_trial = Trial()
# Call the run_trial method of our Trial object
my_trial.run_trial()Run Number 0
Q Time Recep Time with Recep Q Time Nurse Time with Nurse \
Patient ID
1 0.000000 0.164455 0.000000 13.920914
2 0.000000 0.517079 12.717109 7.064436
3 0.000000 3.507019 13.651053 2.107220
4 1.791675 1.914879 13.843393 4.172893
5 2.942190 7.578821 10.437466 3.408435
6 0.000000 0.137868 5.492462 0.770591
7 0.000000 0.038824 4.238580 2.573929
8 0.000000 4.497553 0.000000 3.634398
9 0.632419 1.127904 2.506494 10.751089
10 0.000000 1.827010 9.859928 2.064096
11 0.000000 2.691982 0.000000 5.879487
12 0.000000 4.235160 0.000000 4.587604
13 0.677981 0.348057 4.239547 0.455397
14 0.000000 0.286387 0.000000 18.738572
15 0.000000 2.380793 0.000000 16.075224
16 1.274408 0.609359 15.465865 5.910793
17 0.335087 0.758238 NaN NaN
18 0.000000 1.659091 NaN NaN
19 1.568443 0.213691 NaN NaN
20 0.074793 1.532815 NaN NaN
21 0.000000 2.175654 NaN NaN
Q Time Doctor Time with Doctor
Patient ID
1 0.000000 0.337148
2 0.000000 20.124791
3 0.000000 10.157277
4 5.984384 10.343443
5 10.436243 6.464671
6 NaN NaN
7 NaN NaN
8 0.000000 39.116816
9 0.000000 30.225136
10 NaN NaN
11 NaN NaN
12 14.854357 5.365691
13 16.258368 2.616966
14 0.000000 9.841665
15 0.000000 5.992586
16 NaN NaN
17 NaN NaN
18 NaN NaN
19 NaN NaN
20 NaN NaN
21 NaN NaN
Trial Results
Mean Q Time Recep Mean Q Time Nurse Mean Q Time Doctor
Run Number
0 0.442714 5.778244 4.321214